Finite State Machines (FSM) can be an awesome tool when creating software. Creating FSM’s, is typically split into multiple phases, the first being trying to visualize the workflow the FSM is representing. This is often done using “state diagrams”. Let’s have a look at an example. The following diagram is for a state machine, taking in an input string, and trying to match the 4th, 8th, 12th etc. ‘1’ in an input string.
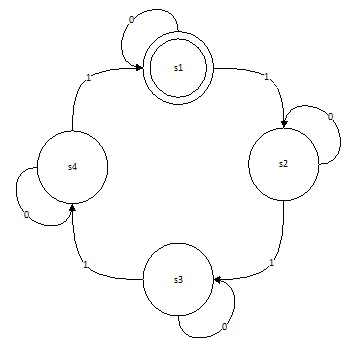
So the STM will keep looping around, until it finds a multiple of 4th ‘1’ in an input string with the input possibilities of 0 and 1.
Using discrete math, we can break down this behavior, into the following definitions.
I = [0,1]; % the possibilities of input.O = [0,1]; % the possibilities of output. (0, for each input except for the 4th, 8th, 12th etc. 1)Then we can define a Matrix, ns, with the transition between states, based on input value. Aka. Next state.
ns =| input | 0 | 1 |
|---|---|---|
| s1 | 1 | 2 |
| s2 | 2 | 3 |
| s3 | 3 | 4 |
| s4 | 4 | 1 |
And lastly, we can define the result matrix, ? (omega)
w =| input | 0 | 1 |
|---|---|---|
| s1 | 0 | 0 |
| s2 | 0 | 0 |
| s3 | 0 | 0 |
| s4 | 0 | 1 |
The two matrices, are built in a way, that makes it easy to find the next state from the current state and input value, as well as finding the output value based on current state and input value. Let’s have an example: If our current state, is s1 and input value is 1. Then our lookup from next-state will be state = ns[1,1] or in a more general term: State = ns[state,inputvalue] The same goes for our result matrix, ω as: result = ω[state,inputvalue] These characteristics we can utilize in MatLab, to create a generic FSM function which takes a range of arguments:
function [y] = fsm(I,O,omega,ns,s1,x)I being the valid input values vector, e.g. [0,1] O being the valid output values vector, eg. [0,1] omega is the omega matrix and ns is the next-state matrix. s1 is the start-state represented by a number and lastly x is the input values as a vector, e.g. [0,0,0,1,0,1,1,0,1,1,0,0]
Let us build up the matric, and see the FSM in action. First off, when building matrices in MatLab, you do it as if they were vectors, however for each column, you break it with a ; instead of a normal comma. Thus creating the matrices omega and ns we put in:
omega = [0,0;0,0;0,0;0,1];ns = [1,2;2,3;3,4;4,1];The input and output vectors are pretty simple, as we expect only 0’s and 1’s, thus both will be defined as:
I = [0,1];O = [0,1];Now we have everything to use our FSM, except for an input string. Since we are supposed to catch the 4th, 8th, 12th etc. ‘1’ in the string, we should have a string which length is long enough to contain at least 12 1s and a number of 0’s. We define x as:
x = [1,1,0,1,1,1,0,0,0,1,1,1,1,1,1,1,0,1,1,0,1,1,1,1,1,1,1,1,0,0,1,0,1,1,0];Now lest call the FSM function, recall the function parameters to be: Input-range vector, Output-range vector, omega, ns, start state and x.
[y] = FSM(I,O,omega,ns,1,x)Our output from the function is pretty long since MatLab automatically adds more text to the output, as it counts the columns. If we wish to make sure out input is correct, we should have a look at the input string (x) and figure out at which positions, the 4th, 8th and 12th ‘1’ is. In this particular case, we have it at the 5th, 12th, 16th, 22nd, 26th and 33rd position. To easily check which positions are ‘1’s in out output in MatLab, utilizes MatLabs Find function. We can do a Boolean match against the values in a vector, and get the positions if we do:
Find(y==1)5 12 16 22 26 33Which compares to our expected result!
